The Steinhart and Hart Equation is an empirical expression that has been determined to be the best mathematical expression for resistance temperature relationship of NTC thermistors and NTC probe assemblies.
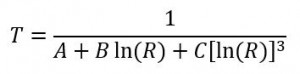
Steinhart and Hart Equation 1
Where:
“T” is in degrees Kelvin and “A”, “B”, and “C” are coefficients derived as follows:
First, measure the thermistor at three different temperatures. The temperatures should be evenly spaced and at least 10 degrees apart. Use the three temperatures to solve three simultaneous equations using these steps:
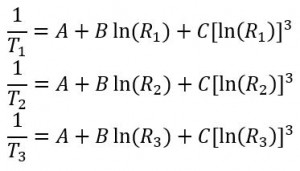
Steinhart and Hart Equations 2-4
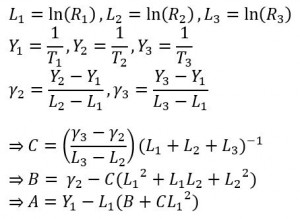
Solving the Steinhart and Hart Equation for Coefficients
Knowing A, B and C for a thermistor allows you to use the Steinhart and Hart equation in two ways.
1) If resistance is known and temperature desired then use Equation 1 above.
2) If temperature is known and expected resistance is desired, use Equation 5 below:
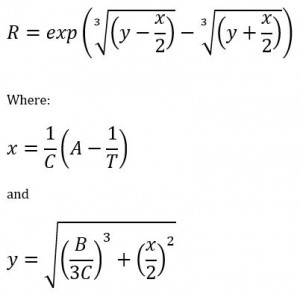
Steinhart and Hart Equation 5




