Thermistors for Temperature Measurement
NTC Thermistors provide an excellent solution in applications requiring accurate temperature measurement. Because of their high sensitivity, NTC Thermistors are ideal for detecting small changes in temperature. However, the characteristic curves for these thermistors are highly non-linear. The resistance is generally an exponential function of the temperature, as shown in Equation (1)
where R0 is the resistance at a reference temperature, T0, while ß is a constant, characteristic of the material, T0, the reference temperature, is generally taken as 298 °K (25 °C).
If the user can measure the resistance electrically, solving for the temperature is easy with the resistance versus temperature curve that Ametherm provides for a specified NTC thermistor.
However, if the thermistor is embedded in a circuit, the resistance changes are recorded in terms of the corresponding voltage or current changes. In this case, the users will have to measure electrical quantities (for example, voltage) first before calculating temperature from such electrical maesurements.
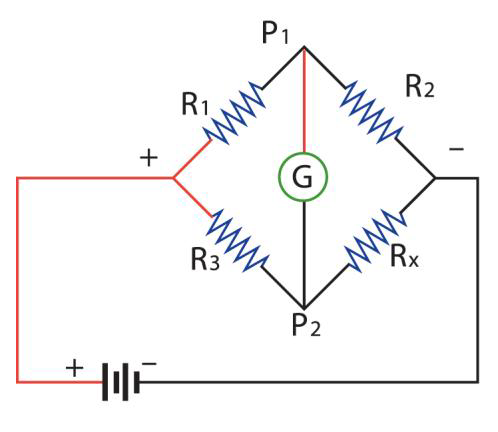
Figure 1: The Wheatstone Bridge
Why Wheatstone Bridge?
A Wheatstone bridge, also called a null comparator, is used for measuring accurate resistance.
In the Wheatstone bridge of Figure 1, R1, R2, and R3 are known and Rx is the unknown resistance. When the potential (voltage) P1 (see the figure) is the same as potential P2, the bridge is said to be balanced.
In this condition, no current flows (as indicated by the “zero” reading of the meter) through the galvanometer and the ratio of resistance in the Rl – R2 path must equal the ratio in the R3 – Rx path.
The major challenge of accurate resistance measurement is to alleviate the loading effect of the circuit by the meter.
Such an inaccuracy is caused by the drawing of power by the meter, although the amount of power drawn is negligibly small, from the circuit, even if it has a very high-impedance (e.g 10 MΩ).
For accurate measurement of Rx, the Wheatstone bridge plays a great role, as the galvanometer, in balanced condition, does not draw any power from the circuit. This increases accuracy by alleviating the “loading” effect of the circuit by the meter.
The Wheatstone bridge is called a null comparator because it makes a measurement by comparing two quantities, one of known value, the other unknown.
The unknown value is adjusted untill it equals the known value and the detector placed across them gives a zero or null reading.
The following condition holds for the balanced Wheatstone bridge:
Measuring Temperature With The Wheatstone Bridge
For measuring temperature, a Wheatstone bridge is used in out of balance where the out-of-balance voltage, ΔV, can be measured and related to the resistance of the thermistor. See this simple DC bridge circuit as shown in Figure 2 that is used for such precision measurement using the thermistor. A correct choice of resistors R2 and R3 will remove the mean DC value of ΔV.
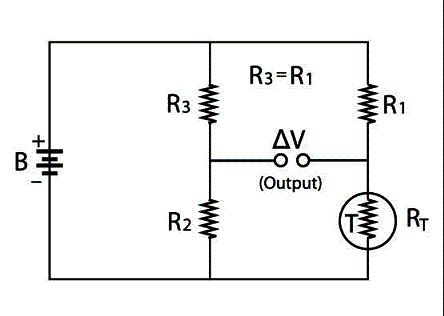
Figure 2. Temperature Measurement Using Thermistors
Considering this circuit, we now derive the relation between T and .V. In general,
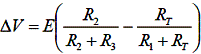
Assume R1 = R3. Then,
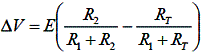
Rearranging for RT,
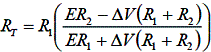
The relation between T and RT is given by,
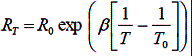
or,
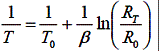
Substituting for RT from Equation 5, we have
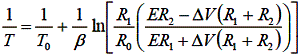
If we further assume R1 = R2 = R3 = Rb, we have
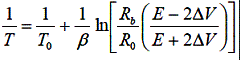 >
>
Although T is not a linear function of voltage, for small ranges in temperatures, it can be considered as linear and the error may be negligible in computing the temperature (See Figure 3). Ametherm provides the value of R0 and ß of Equation 9.
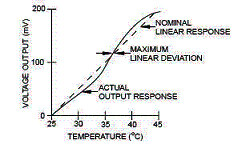
Figure 3: Typical voltage temperature curve from the bridge circuit
Note:
Thermistors are also subject to self heating effects that is not discussed here. Choice of resistors in the Wheatstone Bridge circuit depends on the application and on the temperature measurement range.




